Skip to main content

Mathematics Support

Algebra I | Unit 1 2 3 4 5 6 7

Unit 4

Functions

Functions

 

Videos

Main ideas in this unit

In this unit, students learn about functions, building on their work in middle school. A function is a relationship between an input and an output, where for every input there is exactly one output. Here are some examples of functions:

  • The relationship between a name (input) and the number of letters in it (output). If the input is “Maya Angelou,” the only possible output is 11. 
  • The relationship between the number of seconds since an oven was turned on (input) and the temperature in the oven (output). For example, 50 seconds after the oven was turned on, the temperature in the oven was 124 degrees Fahrenheit.

We often use the phrase “(output) is a function of (input)” to express how the input and output sets are related. For example, “the number of letters in a name is a function of the name,” or “the temperature in the oven is a function of time since it was turned on.”

To make it easier to talk about and work with functions, we often use letters to name them, and we use function notation to represent their input and output. 

Suppose  is a function that tells us the distance, in feet, that a child ran over time, t, in seconds. So: f is the name of the function, time is the input, and distance is the output. 

Here is how we represent this information in function notation:

The notation is read “f of t”.

Here are examples of some things we can say with function notation:

statement meaning interpretation
f(t) the output of f when t is the input the distance run after tseconds
f(3) the output of f when 3 is the input the distance run after 3 seconds
f(6)=14 when the input is 6, the output of f is 14 in 6 seconds, the child ran 14 feet
f(y)=50 when the input is t, the output of f is 50

in t seconds, the child ran 50 feet

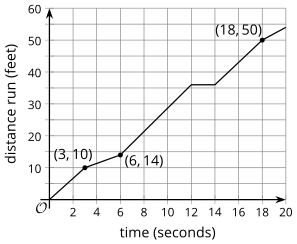
A function can also be represented with a graph. Here is a graph of function f.

We can use it to estimate the input and output values of the function.

For instance, the graph shows that f(3)=10, which means that 3 seconds after she started running, the child has run 10 feet.

We can also use the graph to find out the time when the child has run 50 feet, or the value of t in f(t)=50. We can see that it happened when t is 18.

Sometimes a rule tells us what to do to the input of a function to get the output.

Suppose function gives the dollar cost of buying burritos at $5 each. To get the output (the cost), we multiply the input (the number of burritos) by 5. We can write: g(x)=5x.

Here is a task to try with your student:

The height of a plant in centimeters is a function of its height in inches, .

  1. Let p represent this function. Name the input and output of p.
  2. What does p(10) mean in this situation? What about p(h)=50.8?
  3. Because there are 2.54 centimeters in 1 inch, a rule that defines is p(h)=2.54h. What is the value of p(10)?
  4. What is the value of h when p(h) is 50.8?

Solution

  1. The input is height in inches.The output is height in centimeters.
  2. p(10) represents the plant’s height in centimeters when its height is 10 inches. p(h)=50.8 tells us that the plant is 50.8 centimeters tall when its height is h inches.
  3. 25.4 centimeters. (p(10)=2.54(10)=25.4)
  4. 20 inches

IM Algebra 1 is copyright 2019 Illustrative Mathematics and licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Disclaimer: This site provides external links and videos as a convenience and for informational purposes only. The appearance of external hyperlinks on the MCPS Family Mathematics Support Center website does not constitute an endorsement by the Montgomery County Public School System of any of the products or opinions contained therein.