Representing Situations of the Form PX+Q=R and P(X+Q)=R
In this unit, your student will be representing situations with diagrams and equations. There are two main categories of situations with associated diagrams and equations.
Here is an example of the first type: A standard deck of playing cards has four suits. In each suit, there are 3 face cards and
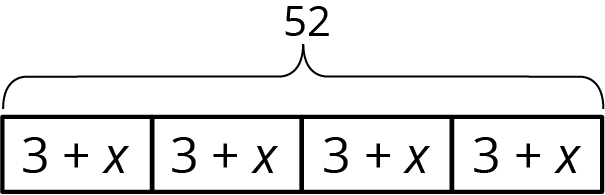
and its associated equation could be
Here is an example of the second type: A chef makes 52 pints of spaghetti sauce. She reserves 3 pints to take home to her family, and divides the remaining sauce equally into 4 containers. A diagram we might use to represent this situation is:
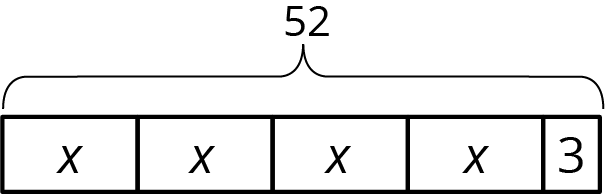
and its associated equation could be
Here is a task to try with your student:
- Draw a diagram to represent the equation
3x+6=39 - Draw a diagram to represent the equation
39=3(y+6) - Decide which story goes with which equation-diagram pair:
- Three friends went cherry picking and each picked the same amount of cherries, in pounds. Before they left the cherry farm, someone gave them an additional 6 pounds of cherries. Altogether, they had 39 pounds of cherries.
- One of the friends made three cherry tarts. She put the same number of cherries in each tart, and then added 6 more cherries to each tart. Altogether, the three tarts contained 39 cherries.
Solution:
Diagram A represents

Solving Equations of the Form PX+Q=R and P(X+Q)=R and Problems that Lead to Those Questions
Your student is studying efficient methods to solve equations and working to understand why these methods work. Sometimes to solve an equation, we can just think of a number that would make the equation true. For example, the solution to
An important method for solving equations is doing the same thing to each side. For example, let's show how we might solve
Another helpful tool for solving equations is to apply the distributive property. In the example above, instead of multiplying each side by
Here is a task to try with your student:
Elena picks a number, adds 45 to it, and then multiplies by
Find Elena’s number. Describe the steps you used.
Solution:
Elena’s number was 13. There are many different ways to solve her equation. Here is one example:
Inequalities
This week your student will be working with inequalities (expressions with

Here is a task to try with your student:
Noah already has $10.50, and he earns $3 each time he runs an errand for his neighbor. Noah wants to know how many errands he needs to run to have at least $30, so he writes this inequality:
We can test this inequality for different values of
- Will Noah reach his goal if he runs:
- 8 errands?
- 9 errands?
- What value of
e makes the equation3e+10.50=30 true? - What does this tell you about all the solutions to the inequality
3e+10.50≥30 ? - What does this mean for Noah’s situation?
Solutions
-
- Yes, if Noah runs 8 errands, he will have
3⋅8+10.50 , or $34.50. - Yes, since 9 is more than 8, and 8 errands was enough, so 9 will also be enough.
- Yes, if Noah runs 8 errands, he will have
- The equation is true when
e=6.5 . We can rewrite the equation as3e=30−10.50 , or3e=19.50 . Then we can rewrite this ase=19.50÷3 , ore=6.5 . - This means that when
e≥6.5 then Noah’s inequality is true. - Noah can’t really run 6.5 errands, but he could run 7 or more errands, and then he would have more than $30.
Writing Equivalent Expressions
This week your student will be working with equivalent expressions (expressions that are always equal, for any value of the variable). For example,
Row 1 |
|||
|---|---|---|---|
| Row 2 | when |
||
| Row 3 | when |
|
We can also use properties of operations to see why these expressions have to be equivalent—they are each equivalent to the expression
Here is a task to try with your student:
Match each expression with an equivalent expression from the list below. One expression in the list will be left over.
5x+8−2x+1 6(4x−3) (5x+8)−(2x+1) -12x+9
List:
3x+7 3x+9 -3(4x−3) 24x+3 24x−18
Solution
3x+9 is equivalent to5x+8−2x+1 , because5x+-2x=3x and8+1=9 .24x−18 is equivalent to6(4x−3) , because6⋅4x=24x and6⋅-3=-18 .3x+7 is equivalent to(5x+8)−(2x+1) , because5x−2x=3x and8−1=7 .-3(4x−3) is equivalent to-12x+9 , because-3⋅4x=-12x and-3⋅-3=9 .
IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.