Skip to main content

Mathematics Support

Investigations Into Mathematics (IM) | Unit 1 2 3 4 5 6 7  

Unit 6

Functional Relationships and Linear Equations


Connecting Proportional Relationships to Linear Equations

Solving Linear Equations

 

Connecting Proportional Relationships to Linear Equations

Students will be able to...

  • Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways.  
  • Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation y = mx for a line through the origin and the equation y = mx + b for a line intercepting the vertical axis at b.

The Common Core State Standards require a balance of three fundamental components that result in rigorous mathematics acquisition: deep conceptual understanding, procedural skill, and mathematical applications and modeling.

 Unit 6 Topic 1 Flowchart

In school, your child will…

  • Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways.

    Compare the scenarios to determine which represents a greater speed.

          Scenarios  

  • Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation y = mx for a line through the origin and the equation y = mx + b for a line intercepting the vertical axis at b.  
    •  Consider any two points (x1, y1) and (x2, y2) on the line shown. Draw a triangle with an equivalent ratio to the three triangles drawn.   
    • What is the slope between these two points?
    • Why should this slope be the same as the slopes of the three other triangles?
    • What is the equation of the line?
     

        Similar Triangles Graph adapted from illustrative mathematics                                                                                                                                                                                  

At home, your child can…

  • Explore more about slope in the real world. 
    • Visit a local bakery to see how similar triangles help create tiered cakes that are pleasing to the eye. Try it at home. Visit Finding Math in cake artistry to learn more. 
    • Ramps help launch bikes, snowboards, and skis into the atmosphere. Investigate positive and negative slopes in sport. The video, Skip Jumping: Understanding proportional relationships, investigates slope and its connection to the sport.
    • Investigate the rise and run ratio and compare different staircases in your home and around your community. View the online video, Stairway Step, to get started.  
     
  • Visit the CK12 PLIX (Play Learn Interact Xplore):    

Additional Resources

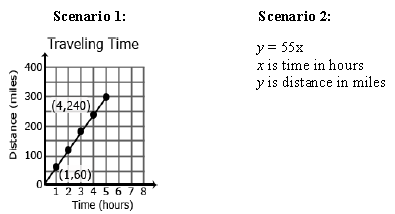
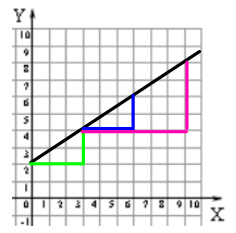
*Additional Practice links support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.

 

Solving Linear Equations

Students will be able to...

  • Solve linear equations in one variable. 
  • Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation of the form x = a, a = a, or a = b results (where a and b are different numbers). 
  • Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms. 

*Instructional videos in the hyperlinks above are meant to support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.

The Common Core State Standards require a balance of three fundamental components that result in rigorous mathematics acquisition: deep conceptual understanding, procedural skill, and mathematical applications and modeling.

 Unit 6 Topic 2 Flowchart

In school, your child will…

  • Solve linear equations in one variable. Compare the Algebra Tile Model and Algebraic Model to solve.    
         Compare Models

  • Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation of the form x = a, a = a, or a = b results (where a and b are different numbers). 
         Solving with the models
 
  • Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.
           Model and Justification

At home, your child can...

  • Examine a linear equation and see how properties are used to transform equations. Visit the CK12 PLIX (Play Learn Interact Xplore):    
  • Interpret a model of a real world problem and use it to transform the algebraic equation. Visit the CK12 PLIX (Play Learn Interact Xplore):   
  • Ask your child to describe to you how one can use patterns in an equation to help predict the number of solutions the equation will have. 

Additional Resources

*Additional Practice links support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.

IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.

Disclaimer: This site provides external links and videos as a convenience and for informational purposes only. The appearance of external hyperlinks on the MCPS Family Mathematics Support Center website does not constitute an endorsement by the Montgomery County Public School System of any of the products or opinions contained therein.